Baccalauréat septembre 2011 MATHÉMATIQUES Série ES
sujet : France Métropolitaine
correction de l'exercice 3 : commun à tous les candidats
Une entreprise fabrique chaque mois x tonnes d'un certain produit, avec x appartenant à l'intervalle . Le coût moyen de fabrication, exprimé en milliers d'euros, pour une production mensuelle de x tonnes est donné par , où C est la fonction définie par
À l'aide de la calculatrice :
conjecturer en terme de variations l'évolution du coût moyen de fabrication sur l'intervalle ;

L'observation de la courbe représentative de la fonction C obtenue à la calculatrice, permet de conjecturer les variations de la fonction C
(Choisir comme fenêtre de la représentation : xmin = 0 ; xmax = 6 ; ymin = 0 et ymax = 6)Tableau de variation :
x 0 6 estimer le minimum du coût moyen de fabrication et la production mensuelle correspondante ;
Après le tracé de la courbe représentative de la fonction C il est possible d'obtenir une estimation du minimum de la fonction à l'aide de la calculatrice comme on peut le voir sur les copies d'écran ci-dessous :
Menu calcul choisir l'option minimum Borne inférieure : saisir 1 Borne supérieure : saisir 6 Estimation du minimum 


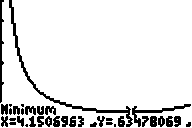
Il semblerait que le coût moyen minimal soit d'environ 635 € obtenu pour une production mensuelle de 4,15 tonnes.
dire s'il est possible d'atteindre un coût moyen de fabrication de 4000 euros. On précisera la méthode utilisée.

La droite d'équation coupe la courbe représentative de la fonction C en un point donc l'équation admet au moins une solution.
Il est possible d'atteindre un coût moyen de fabrication de 4000 euros pour une production mensuelle d'environ 0,504 tonnes.
On désigne par la fonction dérivée de la fonction C. Montrer que, pour tout nombre réel x appartenant à l'intervalle :
La fonction C est dérivable sur l'intervalle comme quotient de deux fonctions dérivables. d'où avec pour tout réel ,
Soit pour tout réel x appartenant à l'intervalle ,
Ainsi, est la fonction définie sur l'intervalle par
On considère la fonction f définie sur l'intervalle par . On désigne par la fonction dérivée de la fonction f.
Vérifier que pour tout nombre réel x appartenant à l'intervalle , .
Sur l'intervalle la fonction est dérivable comme produit de deux fonctions dérivables. Sa dérivée est de la forme avec pour tout nombre réel x appartenant à l'intervalle , ; ; et
La fonction f est dérivable comme somme de fonctions dérivables et pour tout nombre réel x appartenant à l'intervalle ,
Ainsi, est la fonction définie sur l'intervalle par
Justifier que la fonction f est strictement croissante sur l'intervalle .
Pour tout nombre réel x strictement positif, par conséquent :
donc la fonction f est strictement croissante sur l'intervalle .
Justifier que l'équation admet une seule solution α appartenant à l'intervalle . Donner la valeur arrondie au dixième du nombre réel α.
La fonction f est dérivable sur l'intervalle donc continue sur cet intervalle. D'autre part,
Ainsi, sur l'intervalle , la fonction f est continue, strictement croissante, et . Alors, d'après le théorème de la valeur intermédiaire,Si une fonction f est continue et strictement monotone sur un intervalle , alors pour tout réel k compris entre et , l'équation admet une solution unique α située dans l'intervalle . l'équation admet une solution unique α dans l'intervalle
L'équation admet une seule solution
Déduire des résultats précédents le signe de sur l'intervalle .
Sur l'intervalle , la fonction f est strictement croissante et donc :
− si alors ;
− si alors .
À l'aide des questions précédentes, justifier que le minimum du coût moyen de fabrication est obtenu pour une production mensuelle de α tonnes du produit.
soit avec les notations précédentes, .
Or pour tout nombre réel x strictement positif, donc sur l'intervalle , est du même signe que .Les variations de la fonction C se déduisent du signe de sa dérivée d'où le tableau des variations de C :
x 0 α 6 − + Le coût moyen de fabrication minimum est obtenu pour une production mensuelle de α tonnes du produit, soit environ 4,2 tonnes.
Les documents présentés ne sont pas libres de droits. Vous pouvez les télécharger et diffuser (en indiquant la provenance) à condition de ne pas en faire un usage commercial.